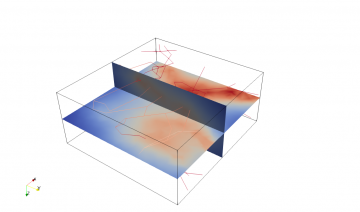
Problemi 3D-1D accoppiati
Problemi alle derivate parziali accoppiati in domini di dimensione diversa e con alto gap dimensionale (3D-1D) emergono in molti contesti applicativi, a valle dell'uso di modelli descrittivi semplificativi. Quando, infatti, il dominio computazionale presenta regioni distinte di forma tubolare aventi diametro piccolo rispetto alla lunghezza e rispetto al dominio, è spesso conveniente operare una riduzione geometrica di tali regioni a domini monodimensionali, immersi nel dominio tridimensionale. Si pensi ad esempio ai casi notevoli della descrizione dei vasi sanguigni in un tessuto, oppure delle fibre all'interno di un materiale fibro-rinforzato. Le regioni filiformi (i capillari o le fibre), inizialmente tridimensionali, vengono descritte come oggetti mono-dimensionali al fine di evitare la generazione di una mesh tridimensionale al loro interno, su una scala molto più piccola rispetto a quella del dominio globale, ottenendo quindi un notevole risparmio di costo computazionale per la simulazione. Questa semplificazione geometrica, però, comporta delle difficoltà dal punto di vista matematico per la definizione di un problema ben posto sul dominio 3D-1D risultante. Inoltre, l'uso di metodi numerici specializzati, su griglie non conformi e basati su tecniche di decomposizione dei domini si rende necessario per offrire soluzioni affidabili ed efficienti.